Why Every Integer Is A Rational Number

Of zero would be any number real or imagined rational or irrational positive or negative an integer or anything in between. Or to put it another way zero is the opposite of any number or number set.

Relationships Between Sets Of Rational Numbers

Find a rational number between 12 and 34.

Why every integer is a rational number. First off integer division is quite a bit faster so if you only need a whole number result one would want to use the more efficient algorithm. Every 1 hexadecimal digit corresponds to 4 binary digits Binary to hexadecimal Hexadecimal to binary 14 1010000100111101 B A 1 3 D H Digit count in binary number not a multiple of 4 pad with zeros on left A 1 3 D H 1010000100111101 B Discard leading zeros from binary number if appropriate Is it clear why programmers. For the third rational expression we will need to avoid m 3 and m - 2.

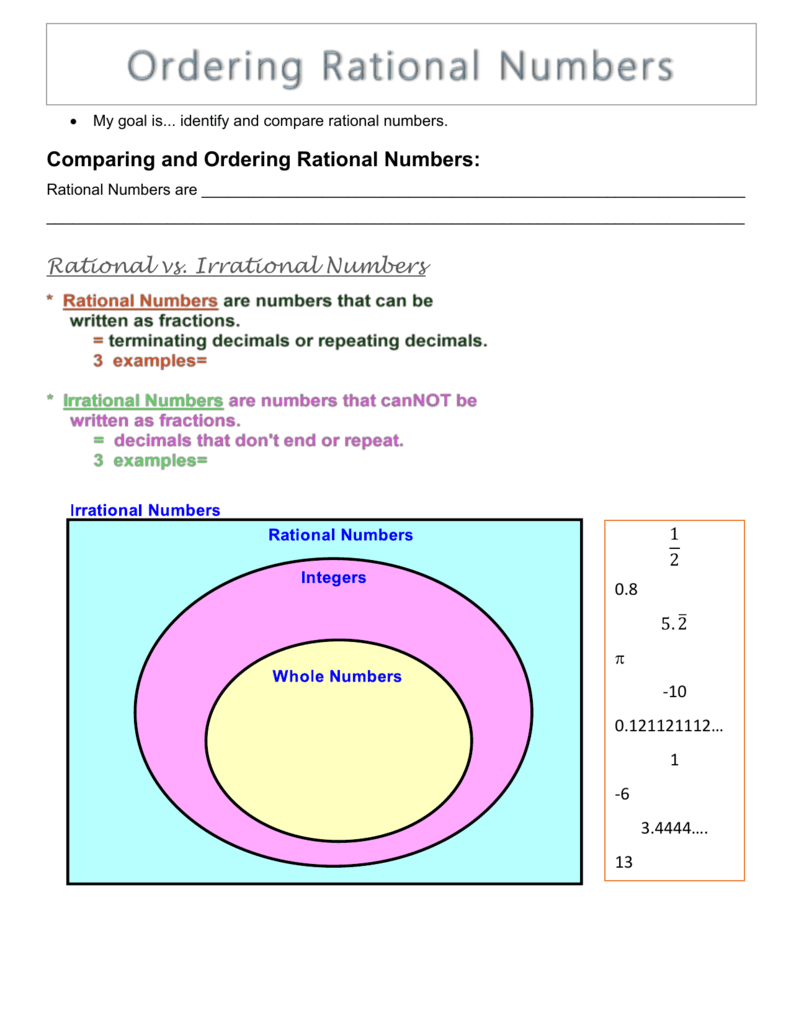
The quotient should be a rational number. 1221 but 12 is not an integer The number. Irrational numbers have an infinite non-periodic decimal part.

03 -025 08976 The following are rational because every repeating decimal. That is okay we just need to avoid division by zero. The following are also rational numbers because a decimal that stops terminates can be written as a rational number.

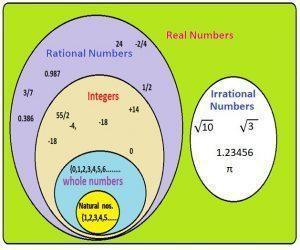
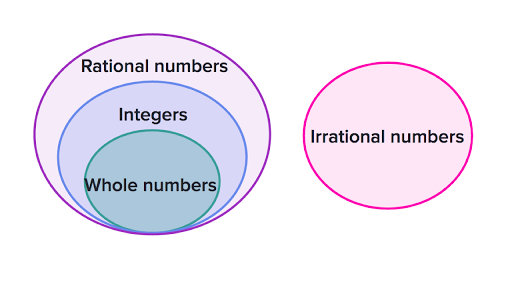
Rational numbers are quantities that sit between integers although strictly speaking integers are a subset of rational numbers because every integer divided by 1 is by definition a rational number as well. We have lots of kinds of numbers but they all start with the natural numbers which are 1 2 3 and so on. Iii Every rational number is a whole number.

Cardinality The cardinality of the set of integers is equal to ℵ 0 aleph-null. Because zero is an integer it fits into many different algebraic number systems like whole natural rational and real numbers. Set of integers is a subset of rational numbers.

Find the sum of first 50 natural numbers. A rational number is any real number that can be expressed exactly as a fraction whose numerator is an integer and whose denominator is a non-zero integer. Zero is also an integral part of the additive identity property which states that the numeral sum of adding zero to any number is the number itself.

In mathematics there are many categories of numbers where the number 1 falls. The following are also rational numbers because a decimal that stops terminates can be written as a rational number. But it will completely miss real roots that are not rational like the roots of x²20 which are 2 or the roots of x²40 which are 2i.

So basically everything except zero is the opposite of zero. Rosa Roberto Andrea and Inno find an estimate for the square root of 10. R is the set of real numbers ie.

Three times the first of three consecutive odd integers is 3 more than twice the third. Global Strategy Stage GloSS and Individual Knowledge Assessment of Number IKAN Prezi. 03 -025 08976 The following are rational because every repeating decimal.

Suppose now that n is not a square number we want to show that the square root of any non-square number is irrational. Integers and floating points are separated by the presence or absence of a decimal point. The answer to this is present in the.

This is because since the integers can be expressed as a quotient of two integers then it is a rational number. Other integer data types are implemented with a fixed size usually a number of bits which is a power of 2 4 8 16 etc or a memorable number of decimal digits eg 9 or 10. To tell if the number was an integer I converted the float number you get from square rooting the user input to a rounded integer stored as the value if those two numbers were equal then the first number must have been an integer allowing the program to respond.

Mike hiked to Big Bear Lake in 45 hours at an average rate of 3 frac15 miles per hour. The second rational expression is never zero in the denominator and so we dont need to worry about any restrictions. In mathematics the irrational numbers from in- prefix assimilated to ir- negative prefix privative rational are all the real numbers which are not rational numbersThat is irrational numbers cannot be expressed as the ratio of two integersWhen the ratio of lengths of two line segments is an irrational number the line segments are also described as being incommensurable.

For instance 5 is an integer whereas 50 is a floating-point number. So 1 can also be called by any of the following numbers. They are defined as int float and complex classes in Python.

If sqrtn is an integer then sqrtn must be rational. Is the logarithm of base transcendental irrational for every integer greater or equal than two. Which statement is false1 point aevery integer is a real number bthe number zero is a rational number cevery irrational number is real number devery real number is a rational number.

It could be a number set an irrational array an equation or a postulation. 11 What Are Numbers. This may not be the shortest way of doing this but it worked for me.

The number 2 has a multiplicative inverse in the set of the rational or real numbers 12. All numbers that can actually exist it contains in addition to rational numbers non-rational numbers or irrational as pi or sqrt2. What is the third integer.

Note as well that the numerator of the second rational expression will be zero. Secondly there are a number of algorithms that use integer division and if the result of division was always a floating point number you would be forced to round the result every time. Applying Rational Number Operations Guided Practice Page No.

Why is 1 Not a Composite Number. That is a rational number is a fraction where a is an integer and b is an integer other than zero. Who has proposed the best solution.

I True The collection of all natural numbers and 0 is called whole numbers. Finally remember that the Rational Root Test works only if all coefficients are integers. Ii Every integer is a whole number.

0 Calculating the base-2 logarithm given an n-bit normalized fractional number. If one-third of one-fourth of a number is 15 then what is the three-tenth of that number. Ii False Negative integers are not whole numbers.

Since sqrtn is an integer we can conclude that n is a square number that is for some integer a. Therefore if n is a square number then sqrtn is rational. If you count your figures and toes you will come to 20 most of you will and that is a natural number.

In decimal form a rational number is either a terminating decimal such as 2 1375 and. Remember the Rational Root Test guarantees to find all rational roots. What is the formula of tanA - B.

Python supports integers floating-point numbers and complex numbers. Number Data Type in Python. Number 1 is not the prime nor the composite number.

Rational Numbers Mathematics Quizizz

Classification Of Numbers Video Practice Questions

Rational Numbers And Integers Rational Numbers Integers Whole Numbers

How To Classify Each Number As Natural Whole Integer Irrational Or Real Math Frac 12 3 Math Math 15 Math Math Frac P 2 Math Math 891 Math Math 3 3 Math Quora

Topic 2 Integers And Rational Numbers Diagram Quizlet

Is Every Rational Number An Integer Quora

Every Integer Is A Rational Number Brainly In

Classifying Numbers Review Article Khan Academy

Rational Numbers Assignment Point

Every Integer Is A Rational Number But A Rational Number Need Not Be An Integer Youtube

Integers Rational Numbers

Every Rational Number Is An Integer It Is True Or False Youtube

Every Integer Is A Rational Number How To Discuss

Is 0 3 A Whole Number A Rational Number An Integer Or A Natural Number List All Of The Answers That Apply Quora