Proof Of Fractional Exponents

Juli 13, 2022 Posting Komentar

F x 1 x. Now we will use the exponent property shown above.

World Web Math Fractional Exponents

Lets make a generalization of this example.

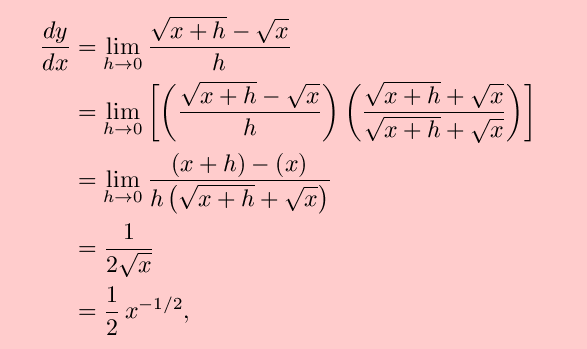
Proof of fractional exponents. Rational number ncan be expressed as pqfor some integers pand nonzero q. We will be looking at more complicated examples after the properties. The derivative of x p q xpq x p q is p q x p q 1 fracpqxpq-1 q p x p q 1.

Multiplying fractional exponents with different exponents and fractions. 52 1 52 1 25 43 1 43 1 64 1 64 5 2 1 5 2 1 25 4 3 1 4 3 1 64 1 64. A nm b kj.

1 the binomial theorem for fractional exponents is due to newton. Sqrtn x x frac 1 n frac 1 n is another way of asking. Exponent we simply need to take the reciprocal of the index of the radical.

3 rows Fractional Exponents. A base number raised to some exponent or the value answer you get if you calculate a number raised to some exponent. For example 8 is a power of 2 since 2 3 8.

We will first rewrite the exponent as follows. 2 32 2 43 2 3243 7127. Use this for prooving the derivatives of xn where n belongs to real nos sothat We will be ready with all the derivatives of xn and hence we can use taylors theorem for prooving the Binomial theorem.

This is the same as x x. If an exponent of a number is a fraction it is called a fractional. A nm a kj a nm kj Example.

Below is the general formula for a fractional exponent with a numerator of 1. Y x a b d e f. The online proofs Ive seen for fractional exponents goes as follows.

In this case ymay be expressed as an implicit function of x y3 x2. Multiplying fractional exponents with same base. One part is 106 and another is 102.

Accompanying each property will be a quick example to illustrate its use. To which I had the proof for all n fractional natural. For example the following are equivalent.

So this is 8 to the 13 third is 2. Using the product rule we find the power rule for the derivative of fx xmn where m and n are positive integers. The exponent is the little elevated number.

Also if we were to presuppose that it is true that the negative exponents are to be writen as fractions in the power of the radix then this current proof would be easily demonstrated by showing that zn z-n z0 by the addition of exponents and zn z-n zn zn 1 by the inversion of negative powers then z01. About functions with fractional exponents such as y x23. The power rule in calculus can be generalized to fractional exponents using the chain rule.

Then This is seen to be consistent with the Power Rule for n 23. When you have a fractional exponent the numerator is the power and the denominator is the root. In this case 3 is the exponent and 2 3 the entire expression is a power.

8 to the 13 is 2 and then were going to square that. Now let f x 1 x. A power is the whole thing.

When we expand it we can see that. 2 32 3 32 23 32 6 32 6 3 216 147. Note that we can rewrite 49 as 491 since they are equivalent you will see in a minute why this.

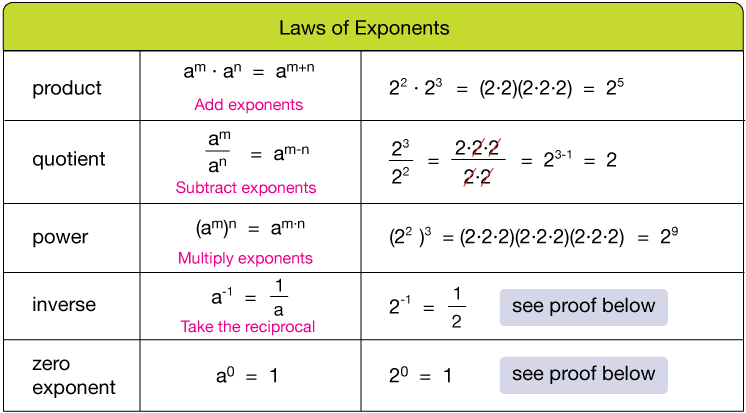
The rule for fractional exponents. Since x a b b x a and by your proof for integer exponents x b a b x b a b x a we have x a b x b a. Here are some of the main properties of integer exponents.

As an application we fi. What number can you multiply by. 2 if you want very rigorous proofs of every detail in calculus you should not be reading calculus made easy which is an intuitive presentation.

If x a x b x a b then x 05 x 05 x. You will now learn how to express a value either in radical form or as a value with a fractional exponent. We write the power in numerator and the index of the root in the.

Y b x a y b b x a b y x a b. The number of 10s here is 8 so its also 108. Now let x y.

Now let x y not negative a be arbitrary and b odd. A fractional exponent is another way of expressing powers and roots together. So this is going to simplify to 3 squared over 2 squared which is just going to be equal to 94.

Since logarithms are basically powers we can say that for example 1062106102. Y x 1 b d e f. Then for y xn.

Baca Juga

In the variable example x a b x frac a b x b a where a a a and b b b are positive real numbers and x x x is a real number a a a is the power and b b b is the root. However we will be using it in the opposite direction than what we did in the previous section. 55 1 3 44 1 4 33 1 5 22 1 6 This led us to our notation for expressing radicals using fractional exponents as well as converting fractional exponents back to radicals which we will be focusing on in this lesson.

A nm b nm a b nm. Well 2 times 2 times 2 is 8. Converting an exponent 𝑥 1.

Xn - an. A fractional exponent is an alternate notation for expressing powers and roots together. Lt ___________ na n-1 x-a x - a.

Bm n b1 nm b m n b 1 n m In other words we can think of the exponent as a product of two numbers. Let me do that same orange color. Therefore x 05 x But since 1 1 1 and 1 1 1 with 1 is not equal to 1 how can we say that x x 05 just because it follows an existing trend.

Express the square root of 49 as a fractional exponent. Its easy to imagine how it works for non-fractional exponents. Y b x y x b.

07 Radicals Can Be Written As Fractional Exponents Youtube

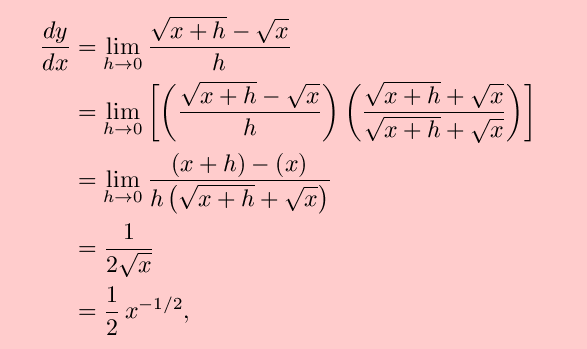
World Web Math Fractional Exponents

1 11 Proof Of Rational Exponents Youtube

How To Do Fraction Exponents Slide Share

Rational Negative Exponents

Fractional Exponents Youtube

How To Do Fraction Exponents By Hand Slide Share

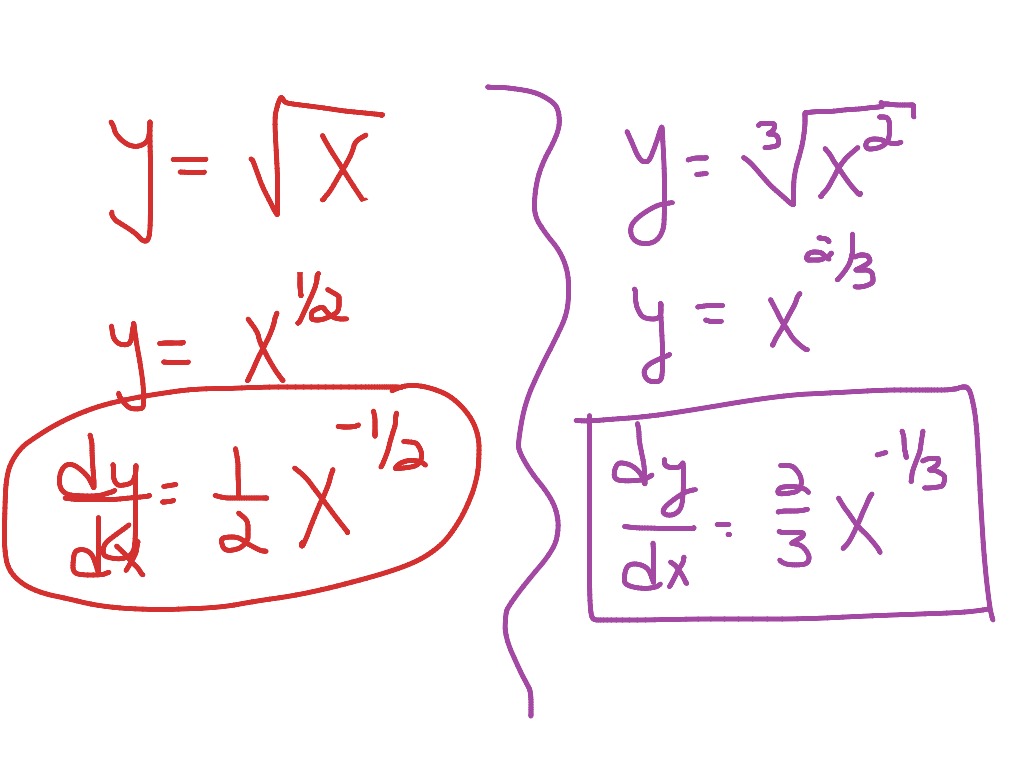
Derivatives Power Rule With Fractional Exponents Math Showme

Fractional Exponents Rule Explained Youtube

What Do Fractional Exponents Mean By Brett Berry Math Hacks Medium

What Are The Laws Of Rational Exponents Mathematics Stack Exchange