Whats An Odd Function

The product of an even function and an odd function is an odd function. What do you mean by harmonics and harmonic analysis in Fourier series.

Odd Function Definition Properties Graph Examples

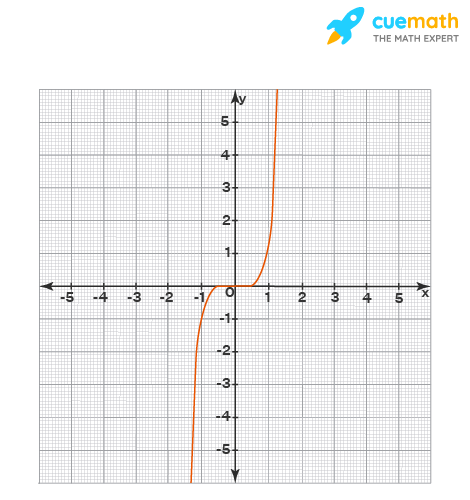
Lets try to observe f x x3 an odd function and see how this affects its table of values.

Whats an odd function. In other words If f x f x f -xf x f x f x the function is even. This algebra 2 and precalculus video tutorial explains how to determine whether a function f is even odd or neither algebraically and using graphs. If a graph is symmetrical about the origin the function is odd.

Algebraically f is odd if and only if f-x -fx for all x in the domain of f. 5 rows The odd functions are functions that return their negative inverse when x is replaced with x. The only function that is even and odd is fx 0.

Test to determine if a function yf x is even odd or neither. Are Constants Even Function. The product of two even or two odd functions is even.

Eqf -x -f x. What is Even Function and Odd Functionmathevenoddmathematicsmathswhat is even functionWhat is Even Function and Odd Functionwhat is odd functionw. If we discover that the function is even or odd the next step is to check the limits of integration the interval over which were integrating.

Mathematics Harvard University 1976. Likewise can a function have no symmetry. A function is called odd if f xf x eg.

If a graph is not symmetrical about the y-axis or the origin the function is neither even nor odd. A function fx is odd if fx -fx ExampleDetermine the nature of the function fx 1x. The definition of even and odd functions.

Odd functions have properties of symmetry that can be useful when graphing and analyzing the functions or when solving equations algebraically. Functions containing odd exponents powers may be odd functions. F -x -x3 x3 This confirms that x f x -x -f x.

Definition of odd function. You may be asked to determine algebraically whether a function is even or odd. The quotient of two even functions is even and the quotient of.

What is the product of an even and odd function. ODD function In which F -x is equal to negative of F x ie. If it goes upwards o Continue Reading Angelos Tsirimokos MA.

Write Two Major Properties of an Even Function. If f x f x f -x-f x f x f x the function is odd. Image will be uploaded soon -f x f -x Or f -x f x 0 If any given function follows the above rule it is said to be an odd function.

This means that if you rotate an odd function 180 around the origin you will have the same function you started with. An odd function is one in which for every element eqx eq in the domain the following property holds. F -X F X This also means that if we draw a graph of the function y f x then the graph will be symmetric or mirror image about the origin.

A functions being odd or even does not imply differentiability or even continuity. A function such that f x f x where the sign is reversed but the absolute value remains the same if the sign of the independent variable is reversed. If f -x f x the function is even.

How do you know if a function is even or odd. This means that f x is an odd function when f -x -f x. The sum of two even functions is even and of two odd ones odd.

The given function is odd if fx. A function fx is even if fx f-x Odd Function. Most functions will be neither even nor odd.

Odd functions If f is a real-valued function on a real set f is even if. A function f is even if the graph of f is symmetric with respect to the y-axisAlgebraically f is even if and only if f-x fx for all x in the domain of f. The graph of any even function is rotationally symmetric.

ODD Function is an inbuilt function in excel as the name suggests it rounds any given number to its odd value the number can be both negative or positive so for example if the given input is ODD-15 the rounded result will be -3 and if the given input is ODD15 then the result is 3. If f -x - f x the function is odd. For example the Dirichlet function is even but is nowhere continuous.

A constant function f x k is an even function because f x k f x. If the function has folded. The other customary context for symmetry is judging from a graph whether a function is even or odd.

Replace x with -x and compare the result to f x. Odd functions are functions that return its negative inverse when x is replaced with x. An odd function is symmetric about the origin 00 of a graph.

To see if a function is even you can imagine folding the graph along its y-axis. For example functions such as f x x 3 f x x 5 f x x 7 are odd functions. A function is odd when f -x f x for all x.

Given equation fx 1x. A function f is odd if the graph of f is symmetric with respect to the origin.

Odd Function From Wolfram Mathworld

Examples With Trigonometric Functions Even Odd Or Neither Video Lessons Examples And Solutions

Even And Odd Degree Polynomials Youtube

Odd Function Definition Properties Graph Examples

Even And Odd Functions Solutions Examples Worksheets Videos Activities

Odd Function Definition Properties Graph Examples

Odd Function Definition Properties Graph Examples

Even Function From Wolfram Mathworld

Odd Function Definition Properties Graph Examples

Even And Odd Functions Tables Video Khan Academy

Mathwords Odd Function

Odd Function Definition Properties Graph Examples

Even And Odd Functions Solutions Examples Worksheets Videos Activities

Odd Functions Odd Function