General Form Of Irrational Numbers

Maret 20, 2023 Posting Komentar

Is an irrational number. If p divides a2.

Rational And Irrational Numbers Digital Math Notebook Digital Math Notebook Studying Math Math Interactive Notebook

An irrational number is a number which is not rational.

General form of irrational numbers. The above statement can be proved using the following theorem. A number that can be expressed as an infinite decimal with no set of consecutive digits repeating itself indefinitely and that cannot be expressed as the quotient of two integers Examples of irrational number in a Sentence. There are equations that cannot be solved using ratios of integers.

The technical definition of an irrational number is that it is a real number which is not a rational number So what does an irrational number look like. Moreover it has been proved that Pi is not an algebraic number ie. For example sqrt2 is not rational thats easy.

Examples of Irrational Numbers 50 is an irrational number with the denominator as zero. E is the limit of 1 1nn as n approaches. As you will find in the Wikipedia article almost all has several different uses.

Operations on rational numbers refer to the mathematical operations carrying out on two or more rational numbersA rational number is a number that is of the form pq where. However he had started using the number in 1727 or 1728. In mathematics the irrational numbers from in- prefix assimilated to ir- negative prefix privative rational are all the real numbers which are not rational numbers.

E also known as Eulers number is another common irrational number. There are no integers p q such that qpi-p0. Thus we can say that non-terminating non-recurring decimals are irrational numbers.

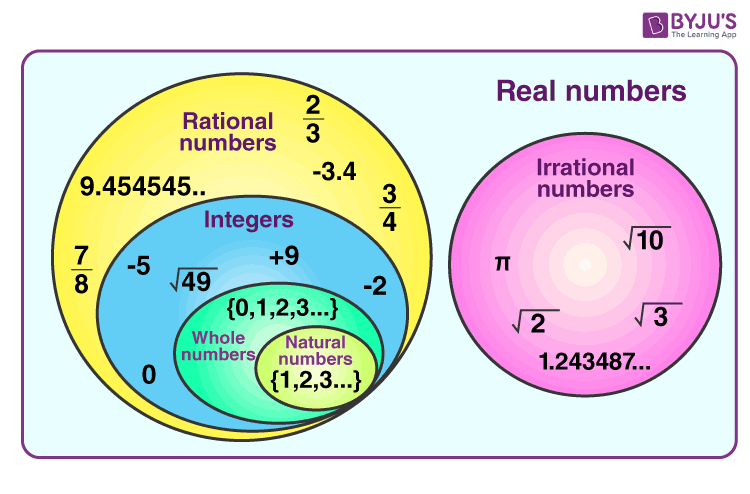
Examples of irrational numbers. Irrational numbers are expressed usually in the form of RQ where the backward slash symbol denotes set minus. An irrational number is a real number that cannot be expressed in the form a b when a and b are integers b 0.

Irrational Numbers 2 Mathematics Assessment Resource Service. Every irrational number is either 9-less or 9-full but not both so almost all irrational numbers are 9-full. In fact the square root of any prime number is irrational.

Some numbers simply cannot be expressed as a ratio of two integers. In this case it means 9-less numbers have Lebesgue measure 0. The ancient Greeks discovered that not all numbers are rational.

1 5 2. And in general if p is a prime number then p. E is a universal number.

The numbers that cannot be represented in P q form where q 0 are known as irrational numbers. Answer 1 of 14. The beginning of this number written out is 271828.

The rational numbers are numbers of the form n where m is an in integer and n a nonzero integer. Roman numerals a system that used combinations of letters from the Roman alphabet remained dominant in Europe until the. Try out examples of different numbers until you form a conjecture about whether the statement is always sometimes or never true.

The first such equation to be studied was 2 x 2. Proof of Irrational Number. 0212112111is a rational number as it.

Pi is not a root of any polynomial with integer coefficients. In other words theyre sprinkled among the irrationals no two touching. In general we can say that the elements of BbbQq_1ldotsq_n are all the numbers of the form Pq_1q_2ldotsq_nRq_1q_2ldotsq_n where P and R are polynomials in n variables with rational integer coefficients such that Rq_1ldotsq_nneq0.

2 is an irrational number as it cannot be simplified. The first few digits look like 161803398874989484820 Properties of Irrational Numbers Addition and Subtraction of Irrational numbers 1. 2 3 5 7.

π is an irrational number which has value 3142and is a never-ending and non-repeating number. Many other square roots are irrational as well. Few examples of irrational numbers are π e φ e This is the Eulers number and also an irrational number.

It has been proved that Pi is not rational ie. Properties of Real Numbers There are four main properties which include commutative property associative property distributive property and identity property. It can also be expressed as R Q which states the difference between a set of real numbers and a set of rational numbers.

Definition of irrational number. In decimal form it never terminates ends or repeats. The square root of any prime number is also an irrational number.

Finding irrational and rational numbers to exemplify general statements. A few examples of irrational numbers are π 2 and 3. These are not rational numbers because either the numerator or the denominator is not an integer.

Methods to Convert the Rational Number into Decimals. These numbers are said to be irrational meaning. That is irrational numbers cannot be expressed as the ratio of two integers.

Irrational numbers Q are numbers that cannot be written as a fraction with the numerator and denominator as integers. The number is named for Leonard Euler who first introduced e in 1731 in a letter he wrote. Let p be a prime number.

Numbers should be distinguished from numerals the symbols used to represent numbersThe Egyptians invented the first ciphered numeral system and the Greeks followed by mapping their counting numbers onto Ionian and Doric alphabets. Eulers number golden ratio and Pi are famous irrational numbers. The first few digits look like 27182818284590452353602874713527 φ This is an irrational number.

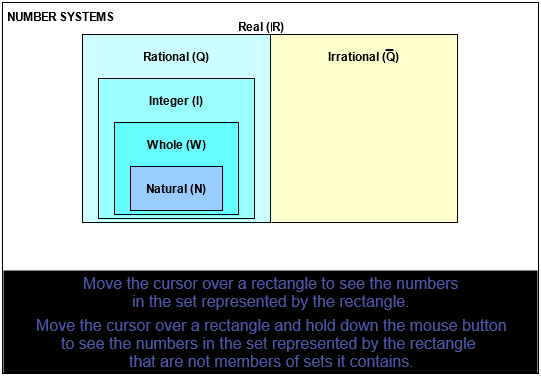
Real Numbers Rational Numbers Integers Whole numbers The Improving Mathematics Education in Schools TIMES Project 5. Irrational numbers are non-terminating and non-repeating in nature like 2 Real Numbers Chart The chart for the set of real numerals including all the types are given below. List of Irrational Numbers All square roots which are not perfect squares are irrational numbers.

Classification Of Numbers Video Practice Questions

How To Convert Irrational Numbers Study Com

Identifying Rational And Irrational Numbers Mathematics For The Liberal Arts Corequisite

Irrational Numbers

Rational And Irrational Numbers Task Irrational Numbers Task Rational Numbers

Guide Students Through The Challenge Of Estimating A Square Root To The Nearest Tenth This Product Interactive Notes Estimating Square Roots Math Interactive