Multiplication Of Radicals Definition

A n b n a b n. What is the product of the product of -22 and 35.

Multiplying Radical Expressions

Multiplying radicals is very simple if the index on all the radicals match.

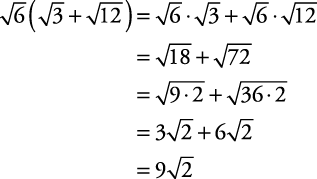
Multiplication of radicals definition. In this tutorial we will look at adding subtracting and multiplying radical expressions. Find the prime factors of the number inside the radical. So we once again see that parenthesis are very important in this class.

Multiplication of Radicals 273. If the denominator is a binomial in which one or both terms contain a square root multiply numerator and denominator by the conjugate. Displaystyle sqrt n atimes sqrt n b sqrt n a b n a.

The product rule of radicals which is already been used can be generalized as follows. Examples 3 4 4 4 3 4 4 12 4 10 5 2 5 10 2 5 20 5. If the denominator is a one-termed radical expression multiply the numerator and the denominator by a radical that will make the radicand of the denominator a perfect-n.

3 x 2 3 x 2 6. Since we know how to evaluate rational exponents we also know how to evaluate radicals as the following set of examples shows. For fg the domains is the intersection of.

RadicalsIf it is simplifying radical expressions that you need a refresher on go to Tutorial 39. Many people mistakenly call this a. When you have a root square root for example in the denominator of a fraction you can remove it multiplying and dividing the fraction for the same quantity.

Learn how to multiply radicals. Sqrt6 cdot sqrt2 Solution. Simplify by multiplication of all variables both inside and outside the radical.

Sqrt6 cdot sqrt2 sqrt6 cdot 2 sqrt12 Example 2. You can multiply if either your radicands are equal or your indexes are equal. When multiplying expressions containing radicals we use the following law along with normal procedures of algebraic multiplication.

Three cases of multiplications of radicals Same indices Different indices but same radicand Totally different in indices and radicands. Multiplication of Radicals STEM Themed Worksheets. When multiplying two radical binomials together the answer can contain no radicals.

For the function f g f - g fg the domains are defined as the inrersection of the domains of f and g. 252 2 x 2 x 3 x 3 x 7. Find the radical index and for this case our index is two because it is a square root.

This pair of binomials with the. Radical quantities may be multiplied like other quantities by writing the factors one after another either with or without the sign of multiplication between them. 1To divide two radicals having the same index use and simplify.

1To multiply two or more radicals having the same index use. The product rule dictates that the multiplication of two radicals simply multiplies the values within and places the answer within the same type of radical simplifying if possible. Simplifying Radical ExpressionsOk I think you are ready to begin this tutorial.

First multiplications when the indexes of radicals are equal. One example of when this can occur is when the two binomials are the same except for the sign in the middle. 91 Thus the product of a into b is a.

Be careful with them. Cube root of number is a value which when multiplied by itself thrice or three times produces the original value. A radical is a symbol that represents a particular root of a number.

Fg x f xg x Multiplication. To multiply radicals with the same root it is usually easy. -23 25 610.

22 x 35. A Quick Intro to Multiplication of Radicals. F - g x f x - g x Subtraction.

Multiplication of Radicals. Radicals - The symbol sqrtnx used to indicate a root is called a radical and is therefore read x radical n or the nth root of x In the radical symbol the horizontal line is called the vinculum the quantity under the vinculum is called the radicand and the quantity n written to the left is called the index. Therefore we need two of a kind.

A radical is an expression or a number under the root symbol. Radicals multiplication of radicals simplified form. For example sqrt32 sqrt34 sqrt38.

Therefore the radical form of this is 8x 1 10 8 10x 108x 8 x 1 10 8 x 10 8 x 10. You can remove the square root multiplying and dividing by sqrt2. One has a plus and the other has a minus.

Multiplying radicals is a bit different. 45 9 x 5 35 24 -4 x 6 26. Definition of a Radical Expression In mathematics a radical expression is defined as any expression containing a radical symbol.

F g x f x g x Addition. The idea is to avoid an irrational number in the denominator. This means that if the index on the radicals match then simply multiply the factors outside the radical and also multiply the factors inside the radicals.

Same indices 𝑥𝑛 𝑦𝑛 𝑥𝑦𝑛. Sqrt06 cdot sqrt5 Solution. Its index is always 2.

Fg x f xg x Division. This property is used to simplify multiplication of radicals. The square root of a number is another number which produces the first number when it is multiplied by itself.

2To multiply radicals with different indices use fractional exponents and the laws of exponents. Definition for Operations on Functions. If you need a review on what radicals are feel free to go to Tutorial 37.

Recall the multiplication property from Lesson 18.

Multiplying Radicals Examples Solutions Videos Worksheets Solutions Activities

Learn How To Multiply Radicals Kate S Math Lessons

Multiply Radicals Questions With Solutions For Grade 10

How Do You Multiply Two Radicals Virtual Nerd

Learn How To Multiply Radicals Kate S Math Lessons

Multiplying Radical Expressions Chilimath

Multiplying Dividing Radical Expressions Youtube

Multiplying Radical Expressions

Multiplying And Dividing Radical Expressions

Multiplying And Dividing Radical Expressions

Multiplying And Dividing Radical Expressions

Multiplying Radical Expressions With Variables And Exponents Youtube

Multiplying And Dividing Radical Expressions

Dividing Radicals Example Solutions Videos Worksheets Games Activities